Virtual relative velocity
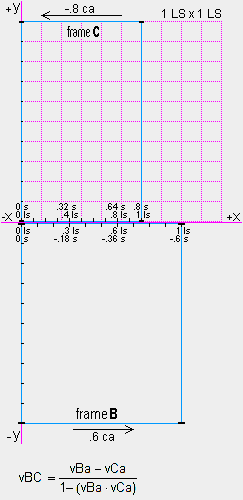
     We determined that observers on frame B observed their correct velocity relative to frame A at rest in the qm. We now show that when two frames are both moving through the qm, observers(c) on the frames observe a virtual relative velocity between the frames that is not their correct, absolute relative velocity. Frames B and C are shown with absolute velocities of .6 ca and −.8 ca respectively along the x axis of a 1 LS x 1 LS grid at rest in the qm. Therefore, the velocity of B relative to C is 1.4 ca. We will see why observers(c) aboard B and C observe a relative velocity less than the speed of light!

     Frame B is .8 LS wide because the physical change ratio for B is .8, as we determined earlier. For frame C, the physical change ratio is rv=(1−.8) or .6. Therefore, the 1 ls distance scale along the x axis of C is only .6 LS long, as shown. At time ta=0 sa, the events [Bx=0:0 is next to Cx=0:0] and [Bx=.6:−.36 is next to Cx=.8:.64] occur. How long will it take for the origin of B to get to the .8 ls mark on C? Because the relative velocity between B and C is 1.4 ca and the distance from the origins to the .8 ls mark on C is (.6·.8) or .48 LS, it will take (.48/1.4) or .342857 sa. During this .342857 sa the clocks on B will advance (.342857·.8) or .274285 s and the clocks on C will advance (.342857·.6) or .205714 s. Therefore, all observers on B and C will see event [Bx=0:.274285 is next to Cx=.8:.845714] (as shown on next page).

     Therefore, the observers on B see the .8 ls mark and clock on C move .6 ls through B in (.274285−(−.36)) or .634285 s and conclude that the velocity of B relative to C is (.6 ls / .634285 s) or .94594 c. Similarly, the observers on C see the 0 ls mark and clock on B move .8 ls through C in (.845714−0) or .845714 s and conclude that the velocity of B relative to C is (.8 ls / .845714 s) or .94594 c. This is the same relative velocity determined aboard B.

     The virtual relative velocity equation (left) specifies the virtual relative velocity (vBC) in terms of the absolute velocity of B (vBa) and the absolute velocity of C (vCa). You can see that the virtual relative velocity is always less than 1 c, even when vBa and vCa are nearly the speed of light and in opposite directions, as are the gold nuclei in the Brookhaven accelerator. Spacetime theory involves virtual relative velocities and the virtual speed of light, c.