How would the acceleration of the 1 kg body appear to observers(c) in an inertial frame that has the va=.6 ca velocity of the body after acceleration? At ta=0 sa the body would appear to have a velocity of .6 c in a direction opposite to the frame's .6 ca velocity. We will designate this the −x direction in the va=.6 ca frame. Before acceleration, the 1 kga body would appear to have a mass of 1.25 kg due to the observed .6 c relative velocity and corresponding "relativistic mass increase." During the 2.25E7 sa acceleration from 0 to .6 ca, the body moved 2.25E15 ma in the +x direction through the qm, but the va=.6 ca frame moved (1.8E8 ma/sa · 2.25E7 sa) or 4.05E15 ma through the qm, so the body moved (4.05E15−2.25E15) or 1.8E15 ma in the −x direction in the va=.6 ca frame. In this reference frame, where rv=.8, the 1.8E15 ma moved by the body is (1.8E15 ma / .8) or 2.25E15 m. And the observed time for this 2.25E7 sa acceleration process is (.8 · 2.25E7 sa + the asynchronization of the clocks for the observed 2.25E15 m or 7.5E6 ls distance) or (1.8E7 s + .6 · 7.5E6 s) or 2.25E7 s.

     Therefore, the observers(c) in the va=.6 ca frame and observers in the qm frame are in exact agreement on the observed distance and time for the acceleration process, but in the qm frame the mass increased and in the va=.6 ca frame the mass appeared to decrease. Because the observers(c) do not understand the cause of the phenomena they observe, it appears to them that a body's mass depends on its velocity relative to an observer and that the body has no actual, absolute mass.

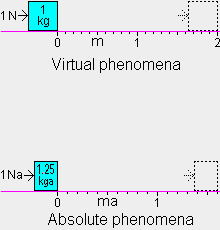
     After the 1 kg body has been accelerated to va=.6 ca and is at rest in the va=.6 ca frame, it can be examined by observers(c) in that frame. They determine the body's mass by applying a 1 N force to the mass and measuring the time for the mass to move 2 m (top figure). They know from f=m·a that if the mass is 1 kg it will have an acceleration of 1 m/s and after 2 s it will have a velocity of 2 m/s and will have moved 2 m because the average velocity is 1 m/s. They measure the time with a stopwatch and find it is 2 s and conclude that the mass is 1 kg.

     The underlying phenomena occurring during the mass measurement are much different (bottom figure). The velocity-changing part of the 1 Na force is f·rv or .64 Na and it causes a .512 ma/sa acceleration of the 1.25 kga mass. After 2 s on the stopwatch (2.5 sa), the body has a velocity of (2.5 sa · .512 ma/sa) or 1.28 ma/sa and has moved 1.6 ma, which is (1.6 ma / .8) or 2 m in the va=.6 ca frame, as seen by observers(c).