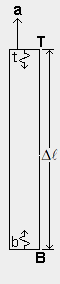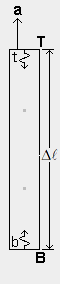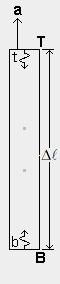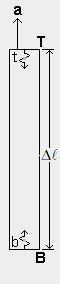
Acceleration and inertial force (faux gravity)
     In the qm view, the inertial force in a body during acceleration is the result of an imbalance in the body's internal energy exchange. The imbalance caused by acceleration is like the imbalance caused by the gradient of rg due to a massive body in the qm. The figure at left shows a box like the one on the previous page within which photons are exchanged between B and T, but there is no mass m or resulting gradient of rg in the qm. The emission frequency and energy of photon b is the same as the emission frequency and energy of t. When the box is at rest in the qm or moving with a constant absolute velocity, the energy absorbed at T when b arrives is the same as the energy absorbed at B when t arrives. There is no imbalance in the energy exchange as long as acceleration a is zero. But when a>0, as shown in the figure, the energy absorbed at B is greater than the energy absorbed at T because, by the time b and t travel distance Δ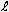, the velocity of b relative to T has been decreased and the velocity of t relative to B has been increased, so that photon b transfers less energy to T than t transfers to B. This results in a net force on the body in a direction opposite to the acceleration.
     The acceleration energy-exchange imbalance (Δea) between B and T, is a function of Planck's constant h, the frequency f of the photons emitted by the body's atoms, distance Δ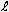, and acceleration a, as follows.
     Using this equation, we can determine the acceleration, a, that will make Δea equal to the Δeg at Earth's surface, which we calculated on page 28 using the rg and Δeg equations. When we make Δ ea=h·f·3.2659E−16 J and Δ 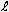=1E−8 LS in the above equation and then solve for the acceleration, a, we get a=3.2659E−8 LS/sa or a=9.8 m/s. This is the acceleration of our box that will cause a virtual gravity inside our box that is equivalent to our box being at rest on Earth's surface. Standing on surface B in the box, we could not tell whether the downward force in our bodies was due to Earth's mass or to acceleration. The qm view explains why 9.8 m/s is also the acceleration toward Earth of a dense object when it is dropped, and it explains why bodies fall with this acceleration regardless of their mass or kind of material. In the qm view, they fall with this acceleration because it results in the balancing of the internal energy exchange. The imbalance caused by the gradient of rg in a body is exactly offset by an equal imbalance in the opposite direction caused by the body's acceleration.