The speed of light cag where rg<1 (and related experimental evidence)
     In the qm view, the speed of light through the qm is reduced by the gravity-causing physical change ratio rg. The reduced speed of light due to rg<1 is designated cag and it is equal to ca·rg, or simply as follows.

cag=rg

     The gradient of rg around a large concentration of mass/energy (e.g. Earth, sun) affects the trajectory of a photon as well as its speed, much as the path of a photon is caused to bend when it passes from air to water where the index of refraction and the photon's speed change. The following equation, in conjunction with the figure at left, specifies the change in photon trajectory.

dxca=dt·(sinθ)·(1−cag)/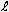

     For example, during a small time increment (dt) sa, a photon p, which is a distance (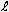) LS from a massive body m, has a velocity (cag) specified by the rg and cag equations. The photon moves a distance of cag·dt LS with an initial trajectory at an angle (θ) to a line to the massive body, as shown. The photon also has a component of motion (dxca) specified by the above equation at right angles to its initial trajectory and toward the massive body, as shown. These two components of motion specify the photon's location p' at the end of the time increment. A line from p through p' specifies the initial trajectory angle for the next time increment. Using this step-and-repeat process, a photon's motion through a gradient of rg in the qm can be computed. The simple rg, cag, and dxca equations are consistent with the following experimental evidence that has been cited to support general relativity theory.

     In the 1960s, radar signals were sent from Earth to Venus and back when Venus was on the far side of the sun so that the signals passed close to the sun where the signals should be slowed due to the sun's large mass. When a signal passed within about 10 LS of the sun's center, the signal was delayed by about 170 microseconds and when a signal passed within about 120 LS of the sun, it was delayed by about 80 microseconds. The time delays specified by the above equations are 182 and 84 microseconds, in general agreement with observations. A calculator for determining the sun's effects on any light path is shown here.

     The bending of the paths of photons due to the sun's mass has also been determined by observing stars and quasars which are seen to pass behind the sun as Earth orbits the sun. The observed bending when a photon's path just grazes the sun's surface is 1.75 arcseconds, and the observed bending when the path comes within 78 LS of the sun's center is .05 arcseconds. The bendings specified by the above equations are 1.746 and .051 arcseconds.