|
|
The anomalous precession of planet orbits in the qm view
A planet's orbit around the sun is closely approximated by an ellipse, and the ellipse is specified by Newton's laws
of motion and gravity. Due to the planet's gravitational interaction with the sun and other planets, its orbit
also precesses (i.e. the orbit rotates) by a small amount. For example, the orbit of Mercury precesses by
about 1.28 arcseconds, asec, per revolution due to the gravitational effects of other planets. This
precession is well understood. However, astronomers observed an additional, so-called "anomalous" precession,
which is about .10 asec per revolution in the case of Mercury. Various attempts were made to explain
this small precession, and eventually relativity theory showed that it could be explained in terms of the curvature
of a mathematical spacetime around the sun.
In the qm view, the anomalous precession is the result of the significant gradient of rg in the qm around
the sun and the gradient's effect on the speeds and paths of the photons and other energy quanta, eq,
that are moving within the planet and also moving through the qm with absolute velocity, cag. (The physical
change ratio, rg, is explained on the
equations page.)
The gradient of rg around the sun influences the paths of all bodies moving through the gradient because it affects
the paths of all eq moving within the bodies and comprising the bodies' total mass/energy. The following
rg, cag, and dxca equations, and the figure below them, specify the effect of the sun on the motions of the eq
comprising a planet's mass/energy. Because a planet's eq are the planet, how they move determines how
the planet moves.
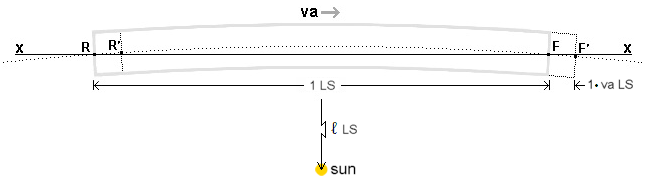
We will consider a simple case of eq transferring energy between the ends of an imaginary box,
as shown by the gray boundaries in the figure below. The centers of the rear and front ends of the box
are designated R and F, and the sun is located at a distance, 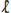 LS, from the
box, as shown. The box is approximately 1 LS long and, due to the sun's 1.989E30 kg mass,
the box has an extremely small curvature, which is shown greatly exaggerated in the figure. (For example,
were the box located at Earth's 500 LS distance from the sun, the box would have a curvature of
1.17 cm over its 1 LS length, or 39 nanometers for every kilometer of distance along
the box.) The curvature is due to the curved paths that all energy quanta take when traveling between
R and F, according to the dxca equation. In the reference frame of the box, the curved path of a
photon traveling through points R and F would appear straight. This path is represented by the dotted line. LS, from the
box, as shown. The box is approximately 1 LS long and, due to the sun's 1.989E30 kg mass,
the box has an extremely small curvature, which is shown greatly exaggerated in the figure. (For example,
were the box located at Earth's 500 LS distance from the sun, the box would have a curvature of
1.17 cm over its 1 LS length, or 39 nanometers for every kilometer of distance along
the box.) The curvature is due to the curved paths that all energy quanta take when traveling between
R and F, according to the dxca equation. In the reference frame of the box, the curved path of a
photon traveling through points R and F would appear straight. This path is represented by the dotted line.
When the box is at rest in the qm (i.e. when va=0 ca), the travel time for the eq traveling between
R and F is the same in both directions (i.e. approximately 1 s).
But when the box is moving with absolute velocity, va, in the +x direction through the qm, the travel time
is greater in the forward direction than in the rearward direction because the
travel distance is longer by approximately 2·(1 s·va) LS because,
during the approximately
1 s eq travel time, F has moved to F' and R has moved to R'. Therefore, locations R and F at the
centers of the box ends follow a curved path through R' and F'. This very small and constantly advancing
eq trajectory angle toward the sun is in addition to the box orbit curvature caused by the
"gravitational attraction" of the box by the sun (which the qm view shows is also due to the gradient
of rg around the sun's mass/energy).
Calculating the anomalous precession of Venus
To calculate how a planet's motion around the sun causes the small anomalous precession, we refer again to the
above figure. We will let the absolute velocity, va, of the box equal the velocity of Venus relative to the
sun. Venus has an orbit radius of about 360.69 LS and a period of revolution around the sun of
about 19414140 seconds (224.7 days). The orbit of Venus is nearly circular, so Venus' speed
around the sun is nearly a constant .00011673 ca. This will simplify our analysis.
To further simplify, we will let the sun be at rest in the qm. (The observed planet orbit precessions
are independent of the sun's motion through the qm, and the reasons for this are similar to the reasons for
observed light speed, c, being independent of the observer's absolute velocity. These complex reasons are explained
here
and elsewhere on this website.) Knowing that the sun's mass is m=1.989e30 kg and that
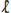 =360.69 LS for Venus, we can use the rg and cag equations
to determine that rg=.999.999.986.37 and cag=.999.999.972.75 ca. =360.69 LS for Venus, we can use the rg and cag equations
to determine that rg=.999.999.986.37 and cag=.999.999.972.75 ca.
Due to the .00011673 ca velocity of the box, the speed of photons and other eq moving from R to F
is .999.883.24 ca relative to the box, and the speed of the eq moving from F to R is
1.000.116.70 ca relative to the box. Therefore, eq moving from R to F take
1.000.116.77 s to travel the 1 LS distance and eq moving from F to R take
.999.883.31 s. Using these travel times for dt in the dxca equation, and knowing
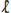 and cag, we can calculate dxca and the amounts that an energy quantum changes
direction when moving from R to F, or from F to R. Due to the difference in travel times, eq moving
from R to F travel farther through the qm and have a greater change in direction than eq moving from F to R.
Due to the greater travel time in the forward direction, dxca in the forward direction is
3.52654e−14 LS greater than dxca in the rearward direction. Therefore, during every second
of box travel, the path of eq between R and F is rotated 3.52654E-14 LS/1 LS or
3.52654E-14 radians. and cag, we can calculate dxca and the amounts that an energy quantum changes
direction when moving from R to F, or from F to R. Due to the difference in travel times, eq moving
from R to F travel farther through the qm and have a greater change in direction than eq moving from F to R.
Due to the greater travel time in the forward direction, dxca in the forward direction is
3.52654e−14 LS greater than dxca in the rearward direction. Therefore, during every second
of box travel, the path of eq between R and F is rotated 3.52654E-14 LS/1 LS or
3.52654E-14 radians.
This incremental change in direction is only for the special case of eq within
Venus having their velocity through the qm parallel to the absolute velocity of Venus and the x axis.
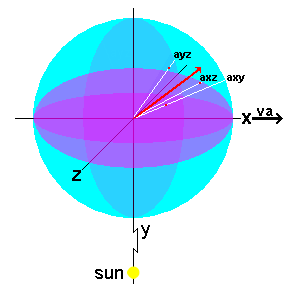
The figure below helps see that essentially all of the energy quanta in a planet are not moving
parallel to va, and for these energy quanta dxca will be less than
calculated above because sinΘ will be less than 1.
For example, for eq moving along lines to the sun, sinΘ=0, dxca=0, and the sun
does not cause any bending of the eq paths.
These eq will not contribute to a planet's anomalous precession.
How can we determine a realistic average bending factor, avgfact, to substitute for sinΘ so that the
resulting dxca will represent the entire planet within which the eq are moving in all directions?
We can start by recognizing that the path bending for eq moving at an angle axy in the xy plane
of the figure will be reduced due to axy's impact on the component of the eq's velocity, cag, in the
direction of va along the x axis. Angle axy also determines angle Θ in the dxca equation.
Therefore, cos(axy) has a large influence on the bending factor for any eq because it specifies a
component of eq velocity that is in the direction of va and is also at a right angle to the y axis
and to a line to the sun. In fact, the bending factor for the sun, sunfact, is simply cos(axy).
The bending factor, vafact, for the planet velocity, va, is more complex. Unlike sunfact,
it is affected significantly by angle axz in the xz plane. When axz is 90°,
vafact=0, and the combined bending factor, sunfact · vafact, is zero.
For any combination of angles axy and axz, vafact = cos(axy) · cos(axz)
is the velocity component of the eq along the x axis.
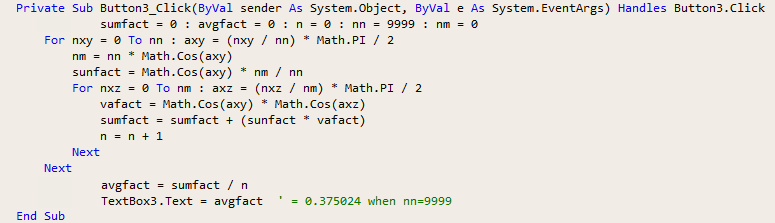
The average eq path bending factor, avgfact, is found by calculating the average of
(sunfact · vafact) for every combination of axy from 0 to 90° and axz
from 0 to 90°. A visual basic program for doing the calculations is shown below.
The program is based on angles axy and axz in an x,y,z coordinate system centered within a unit-radius
sphere. Obtaining uniform spacing between points on this sphere at increasing "latitudes" from the
xz plane requires decreasing the number of points at higher latitudes. This is the reason for
nm=nn·cos(axy), which decreases nm as axy increases. The calculated average bending
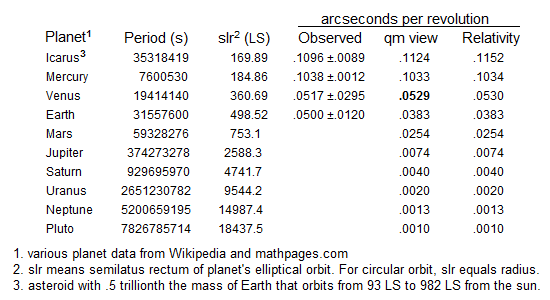
factor is .375, and it results in excellent agreement between the qm view predictions of
planet anomalous precession and the observed precessions tabulated below.
Multiplying the approximately 3.52654E−14 radians/s by .375, we get
1.322454E−14 radians/s. And multiplying by
3600·180/PI to change radians into arcseconds, we get
2.727757E−9 asec of angle change per second. And multiplying by the
19414140 s for Venus to orbit the sun results in a cumulative advancement of Venus's
trajectory of .05295706 asec/revolution, as shown in the following table.
Calculating the anomalous precession of Mercury
We can calculate the expected anomalous precession of Mercury the same way. The minor axis of
Mercury's elliptical orbit is about 98% of the length of the major axis, and to simplify our calculations
we can use the orbit's semilatus rectum as Mercury's distance from the sun. This distance
(which is 1.205 times Mercury's closest distance to the sun and .794 times Mercury's farthest
distance from the sun) is 184.86 LS. This distance and Mercury's revolution period of
7600530 seconds (87.97 days) results in an orbital velocity around the sun of .00015282 c
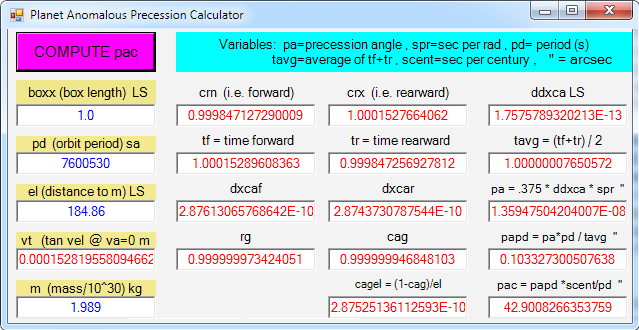
(as shown in the below image of a simple calculator for computing a planet's anomalous
precession after the planets period, pd, and semilatus rectum, el, are specified in the left column).
Just as we did for Venus, we can calculate the rotation of the eq moving within Mercury.
For eq moving in the forward direction (i.e. in va direction), dxca=2.8761306e−10 LS
and for eq moving rearward, dxca=2.8743730e−10 LS, and the difference between these two
displacements is 1.75757e−13 LS. Therefore, the net incremental rotation and
precession of the box and planet is 1.359475E−8 asec/s or
.1033273 asec/revolution (as shown in the table) or 42.9008 asec/century.
This is in close agreement with the generally accepted observed anomalous precession of
43.1 ±.5 arcseconds per century. The anomalous orbit precession for the other
planets and for the asteroid, Icarus, are also specified in the above table, which shows that the
qm view values also agree with the predictions of relativity theory.
Summary and conclusion
The anomalous precessions for the solar system's planets and asteroid, Icarus, were calculated
using the qm view's simple rg, cag, and dxca equations, and the calculated values agree with the
observational evidence and with the predictions of relativity theory.
The fact that the logical consequences of the qm view's two premises permit the anomalous planet
precessions to be explained simply and in terms of logical physical causes is part of the wide variety of
evidence showing that all mass/energy is comprised of oscillating energy quanta moving with the speed of
light through the qm. This fact shows that the mathematical, spacetime theory explanation for the
anomalous precession of planets may be obscuring the physical causes of the phenomenon and thus may be a
misleading representation of nature. This fact is additional evidence that combining two different
fundamental aspects of reality, distance/space and time, into the man-made system of spacetime is
unnecessary.

The anomalous precession of planet orbits in the qm view
© 1994-2015 by P. F. Allport is licensed under a
Creative Commons
Attribution-Noncommercial-Share Alike 3.0 United States License.
|
|
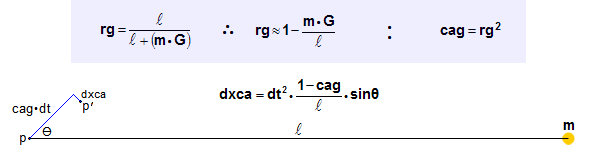
 LS, from the
box, as shown. The box is approximately 1 LS long and, due to the sun's 1.989E30 kg mass,
the box has an extremely small curvature, which is shown greatly exaggerated in the figure. (For example,
were the box located at Earth's 500 LS distance from the sun, the box would have a curvature of
1.17 cm over its 1 LS length, or 39 nanometers for every kilometer of distance along
the box.) The curvature is due to the curved paths that all energy quanta take when traveling between
R and F, according to the dxca equation. In the reference frame of the box, the curved path of a
photon traveling through points R and F would appear straight. This path is represented by the dotted line.
LS, from the
box, as shown. The box is approximately 1 LS long and, due to the sun's 1.989E30 kg mass,
the box has an extremely small curvature, which is shown greatly exaggerated in the figure. (For example,
were the box located at Earth's 500 LS distance from the sun, the box would have a curvature of
1.17 cm over its 1 LS length, or 39 nanometers for every kilometer of distance along
the box.) The curvature is due to the curved paths that all energy quanta take when traveling between
R and F, according to the dxca equation. In the reference frame of the box, the curved path of a
photon traveling through points R and F would appear straight. This path is represented by the dotted line.