Tube and Rod Paradox experiment

Background
This paradox is also known as the "Barn and Pole Paradox" and the "Ladder Paradox." It is the result of the popular belief that relative motion between a body and an observer causes the body to be contracted in the direction of motion through the observer's reference frame. This belief results in the remarkable ability of an observer to cause a body's observed contraction or expansion by changing the observer's motion.

To explain the paradox we will first consider a glass tube that is 1 meter (m) long and an aluminum rod that is 1.1 m long. When the rod is at rest inside the tube, the rod protrudes from the tube, as shown in Fig. 1. But according to relativity theory, if the rod can be made to pass through the tube with sufficient relative velocity, an observer at rest in the reference frame of the tube will see that the entire rod is inside the tube as it passes through.


Specifically, relativity theory says that if the rod passes through the tube with a velocity relative to the tube of 60% of the speed of light (i.e. vRT = .6 c) then the rod will be only .88 m long in the reference frame of the tube, as in Fig. 2.


On the other hand, an observer in the reference frame of the rod will observe that the tube is contracted to .8 m, as shown in Fig. 3. Experimental evidence shows that this conclusion of relativity theory is correct, and this has influenced people to believe that relativity theory is correct. It has influenced them to accept other aspects of relativity theory, including the denial of absolute units of time, distance, and mass. It has, in effect, made reality "observer dependent" because observers moving relative to one another observe different realities because they observe different basic ingredients of reality - - time, distance, and mass.


Quantum Medium View (qm view) explanation for Tube and Rod Paradox
The qm view permits the observers on the tube and rod to agree on the lengths of the tube and rod. In general, it permits all observers moving relative to one another to agree on the times, distances, and masses they observe. In the qm view, the Tube and Rod Paradox and the various other paradoxes that are byproducts of relativity theory are illusions that are logical consequences of a quantum medium that contains all the mass/energy in the universe. The energy exists in the form of oscillations of this medium that propagate through the medium at the absolute speed of light through the medium (ca). Mass/energy systems, which range in size from subatomic particles to clusters of galaxies, are systems of these oscillations, and they move through the medium with various speeds from zero to ca.

A logical consequence of systems of mass/energy comprised of oscillations of the medium is that the exchange of energy within the systems is slowed when the speeds of the systems through the qm are increased. (The energy exchange rate approaches zero as the speed through the qm approaches ca.) This causes all processes within the systems (e.g. atomic clocks) to be slowed. It also causes a foreshortening of the systems in the direction of their absolute velocity (va), which means velocity through the qm. This is explained in the qm view Introduction videos.

Therefore, the lengths of the tube and rod depend on their velocities through the qm. Their maximum lengths occur when they are "at rest" in the qm. As their lengthwise velocity through the qm increases, the ratio of their length to their at-rest length is specified by the following equation where rv is the ratio of their length to their at-rest length and va is their absolute lengthwise velocity in units of ca. This ratio, rv, is known as the "physical change ratio" because it also pertains to other physical characteristics of a system including the system's rate of evolution and mass.


In Fig. 1, when the tube and rod are both at rest in the qm, their lengths are 1 ma and 1.1 ma respectively, where ma is the symbol for an absolute meter which is the length of a standard meter bar at rest in the qm. But if the 1.1 ma rod is caused to move lengthwise with absolute velocity va=.6 ca as shown in Fig. 2, then it's length contracts to (1−.6) 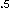or .8 times it's at-rest length per the rv equation. This is a real contraction of the rod due to the real contraction of all the aluminum atoms comprising the rod. The rod continues to be a 1.1 m rod with an at-rest length of 1.1 ma and a variable, 1.1 m length that depends on its motion.

If the rod remains at rest in the qm and the tube is moved lengthwise with an absolute velocity of va=.6 ca as shown in Fig. 3, the tube is contracted to .8 ma. But observers moving with the tube will observe that the tube's length is unchanged and that the rod is foreshortened and fits inside the tube. This observed foreshortening of the rod is a virtual foreshortening or illusion that will be explained below.

Certainly no human could see the tube and rod pass over or through the other because the .6 ca relative velocity is more than 200 000 times the muzzle velocity of a high power rifle. Therefore, we can only imagine this occurring. To make the following explanation of real and virtual foreshortening easier we will imagine a huge tube and rod having at-rest lengths of 1 absolute light-second (LS) and 1.1 LS respectively. When moving through the qm, the absolute lengths of the tube and rod are decreased according to the rv equation but observers on the tube will continue to observe a 1 virtual light-second (ls) tube length and observers on the rod will continue to observe a 1.1 ls rod length. This will become more apparent below.

Distance markers are located every .001 ls along the tube and rod, like distance markers along a highway. Every distance marker location has an atomic clock and an instrumentation system to keep the clock synchronized with a master clock at the 0 ls location on the tube or rod. For example, a clock at a .123 ls location is automatically set to read .123 s later than the time received via radio signal from the master clock. This procedure is consistent with the assumption of constant light and radio signal speed, c, on which relativity theory is based. In the qm view it results in an asynchronization of clocks moving through the qm that will be apparent in the following figures.

This imaginary experiment also requires observers with incredible eyesight or instrumentation that can see the distance markers and the times on the atomic clocks along the tube and rod. Additionally, the clearance between the outside of the rod and the inside of the tube needs to be small so that the time for light to travel between the tube and rod can be ignored.

We will be using absolute and virtual units of length (LS and ls) and time (sa and s) that are defined and/or explained in the Glossary, Equations page, and elsewhere on the qm view website. It is helpful to realize that for any reference frame, or tube or rod at rest in the qm the clocks and distance marks specify absolute times and distances because the absolute velocity is va=0 and the physical change ratio is rv=1. For clocks and distance marks on reference frames or bodies moving through the qm, the physical change ratio, rv, specifies the ratio of (1 sa/1 s) and the ratio of (1 ls/1 LS).

Observations when tube is at rest in qm and rod is moving in +x direction with velocity vRa=.6 ca
Figure 4 shows the rod when it is first completely within the tube. It shows that the experiment has been arranged so that the master clocks at the 0 ls locations on the tube and rod both read 0 s when they are momentarily adjacent to one another. It shows some of the times and distances. Because the tube is at rest in the qm and the speed of light is the same in both directions along the tube, the clocks along the tube are absolutely synchronized. Therefore, the clocks at the ends of the tube read the same time, as shown. Observers on the tube determine that its length is 1 ls because a round-trip light signal between the ends of the tube takes 2 s on the tube's clocks. This 1 ls length is the same as the tube's absolute length in LS.

Similarly, observers on the rod determine that its length is 1.1 ls because a round-trip light signal between the ends of the rod takes 2.2 s on the rod's clocks. In the +x direction a light signal is moving with a velocity of only .4 ca relative to the rod due to the rods .6 ca absolute velocity, and the signal takes (.88 LS / .4 ca) or 2.2 sa to move the .88 LS length of the rod. The return signal takes only .55 sa due to its 1.6 ca relative velocity. Therefore the round-trip time is 2.75 sa or 2.2 s on the rod's clocks due to their .8 physical change ratio.

All observers on the tube can see that the rod is only .88 ls long. They can see that at time 0 s on the tube's clocks one end of the rod was at the 0 ls location on the tube and the other end of the rod was at the .88 ls location on the tube, as shown in Fig. 4.


To understand why observers on the rod determine that the rod is much longer than the tube it is necessary to understand why the clocks along the rod or tube moving through the qm are absolutely asynchronized (i.e. not synchronized) in spite of being virtually synchronized in their reference frames. As shown in Fig. 4, the clocks at the ends of the rod are asynchronized by .66 s due to their .6 ca velocity through the qm and the 1.1 virtual light-second distance between the clocks. The rule for determining this asynchronization is shown on page 12 of the qm view website and the causes of the asynchronization are explained. The Equations page also contains an explanation for the absolute asynchronization after a virtual synchronization of the clocks.

Figure 4 shows that the 0 ls location on the rod is just entering the tube when the clock at this location reads 0 s and when the 1.1 ls end of the rod has .66 s of motion before it reaches its 0 s location. The question we need to answer is, At what location, x LS from the 0 ls end of the rod, will the clock be reading 0 s when it reaches the 1 ls end of the tube? At this x LS location the clock will be displaying the negative of the number of the clock's virtual seconds required for x to get to the 1 ls mark on the tube. Therefore .6 ca · x /.8 = .8 · (1−x) / .6 ca. And (.36 · x = .64 − .64 · x) or x = .64 LS. This .64 LS location is shown on the rod and it is also the .8 ls location where the clock reads −.48 s per the page 12 rule.

During the next .48 s on the rod clocks (i.e. .6 sa) the .64 LS location on the rod moves (.6 sa · .6 ca) = .36 LS from .64 LS on the tube to 1 LS on the tube, as shown in Fig. 5. Therefore, observers and/or instrumentation on the rod (who believe that the clocks on the rod are synchronized) see the tube extending from 0 ls on the rod to .8 ls on the rod when the time on the rod is 0 s, and they conclude that the tube contracted from its 1 ls length when at rest relative to the rod to .8 ls due to its .6 ca velocity relative to the rod.


It has been shown why observers on the tube observe a foreshortened rod that fits within the tube and why observers on the rod observe a foreshortened tube that cannot contain the rod, which are the same conflicting and paradoxical observations predicted and not explained by relativity theory. We will now consider what is observed when the rod is at rest in the qm.

Observations when the rod is at rest in qm and the tube is moving in +x direction with velocity vTa=.6 ca
The qm view explains why the observed foreshortening of the tube by the rod observers is a real foreshortening due to the tube's .6 ca absolute velocity shown in Fig. 6. And we know that the rod observers will observe the real phenomena occurring on the rod and tube because the speed of light in the rod reference frame is constant and isotropic, as the observers assume. But why do the observers on the tube in Fig. 6 observe the long tube and short rod situation as shown in Fig. 2?


The primary reason for the virtual phenomena seen by the tube observers is the large variation in the speeds of light in the tube reference frame. The speed of light in the +x direction is only .4 ca and the speed of light in the −x direction is 1.6 ca. This variation in light speed explains the asynchronization of the clocks on the tube shown in Fig. 6. And the asynchronization of the clocks on the tube explains the short, virtual rod length observed by the tube observers, as follows.

The tube observers and instrumentation all see the 0 ls end of the rod at the 0 ls end of the tube at 0 s on the tube's 0 ls clock, which they observe is synchronized with all the other clocks on the tube. But where on the tube will the clock be reading 0 s when it is at the 1.1 LS end of the rod? Figure 6 shows the x=.704 LS location along the tube that will arrive at the 1.1 LS location on the rod when the clock at the .704 LS location on the tube reads 0 s.

In Fig. 6, the time on the clock at the absolute distance x along the tube where the clock will read 0 s when it arrives at the 1.1 LS location on the rod must be minus (.6 ca · x /.8) virtual seconds (per page 12 rule). This virtual time is equal to the absolute distance that x travels to 1.1 LS on the rod divided by the speed of travel times the physical change ratio for clock x, or .8 · (1.1 − x) / .6 ca. Therefore, (.6 ca · x /.8) = .8 · (1.1 − x) / .6 ca and .36x = .704 − .64x and x=.704 LS and the distance traveled by x is .396 LS. Via the page 12 rule, the time on the clock at x is − (.6 ca · .704 / .8) = −.528 s and the distance traveled to the 1.1 ls location on the rod is (.6 ca · .528 s / .8 s/sa) = .396 LS. The travel time is .528 virtual seconds on the tube clocks and .66 absolute seconds on the rod clocks, as shown in Fig. 7.


Observations when vTa = 1/3 ca and vRa = -1/3 ca
When the absolute velocities of the tube and rod are both 1/3 ca but in opposite directions, the relative velocity observed aboard the tube and rod will be .6 c, as explained in the "Virtual relative velocity" section on the Equations page. The tube and rod will have the same physical change ratio, rv, and will therefore have the same foreshortening per unit length. However, the tube observers will observe the long tube and short rod as shown in Fig. 2, and the rod observers will observe the short tube and long rod as shown in Fig. 3. This will not be explained in detail, but the reader should have enough information to verify that this will be the outcome of an experiment with tube and rod having 1/3 ca velocities in opposite directions (or any other combination of absolute velocities that result in a virtual, observed relative velocity of .6 c).

Would a distant video camera show the rod longer or shorter than the tube?
If the camera is at rest in the qm (e.g. at 100 LS on the y axis) and the tube and rod each have an absolute velocity of 1/3 ca but in opposite directions, then the video pictures will show the rod 10% longer than the tube and therefore unable to fit completely within the tube. If the camera has the same absolute velocity as the tube, then the pictures will show the rod 12% shorter than the tube and therefore fitting completely within the tube. And if the camera has the same velocity as the rod, then the pictures will show the rod 37.5% longer than the tube.

So, does the rod fit within the tube or not? This is a question that relativity theory cannot answer. In the qm view, relativity theory provides an incomplete picture and erroneous understanding of what is occurring as the tube and rod move with a virtual velocity of .6 c relative to one another. The answer depends on the absolute velocities of the tube and rod. The tube and rod will have the same length when rv for the tube is 10% larger than rv for the rod. The combination of absolute velocities for the tube and rod that satisfy this requirement and also result in a .6 c virtual relative velocity between tube and rod are vTa=.2 ca and vRa=.454545... ca in the opposite direction. Therefore, any vTa less than .2 will result in the rod fitting within the tube because vRa will be more than .454545..., which will make (rvT / rvR) greater than 1.1, which results in the rod being shorter than the tube and fitting completely within the tube.

Whether or not the rod is shorter than the tube can be determined only if we know the absolute velocities of the tube or rod or the video camera or our absolute velocity, which we can currently only estimate. Probably Earth's absolute velocity is very low relative to the speed of light. One indication is the cosmic microwave background radiation which is probably isotropic in the quantum medium reference frame. On Earth the CMB is observed to have a dipole which would occur if Earth is moving through the CMB with an absolute relative velocity of about .0012 ca. Therefore, if we observed the tube moving relative to us with a velocity somewhat less than .2 c we could be confident that the rod is shorter than the tube.

Summary
A purpose of this imaginary tube and rod experiment is to encourage readers to consider if relative motion between the tube and rod is the real cause of the observed foreshortening of the rod and/or tube, bearing in mind that any independent observer can change the observed lengths of the tube and rod (e.g. make them the same length) by adjusting the observer's motion. How is this physically possible? Relativity theory does not reveal how this is physically possible.

How can an observer, who could be light years away from the tube and rod change their lengths or have any immediate physical effect on the tube or rod? We think it is reasonable to conclude that the observer's motion has no influence on the tube and rod and that a change in the observers motion must change something in the observer's system, not the tube's or rod's systems. What possible change could occur in the observer's system as a result of changing the observer's velocity? The qm view shows that a change in the observer's velocity causes a change in the rates of energy transfer through the observer's system, which changes the physical standards of time and distance in the observer's system. Unless observers moving relative to one another understand this and convert their virtual units of time, distance, and mass into absolute units, their observations will disagree with one another. If the observers on the tube and rod understood this they could agree on the absolute lengths of the tube and rod regardless of their absolute velocities, and the paradox caused by the light speed, c, assumption would no longer be a concern.