Clock Asynchronization Rule:
In any inertial reference frame moving through the qm, two clocks which have been virtually synchronized are out of sync by an amount equal to the absolute velocity of the reference frame times the observed ls distance between the clocks in the direction of absolute motion. The forward clock is retarded relative to the rearward clock.

The slowing and asynchronization of clocks on B

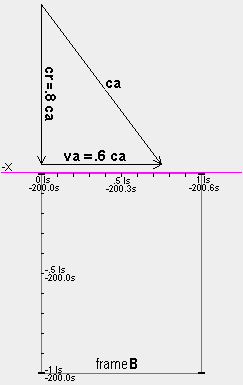
     Frame B's .6 ca absolute velocity causes the speed of light in B to range from .4 ca in the +x direction to 1.6 ca in the −x direction. In the +y and −y directions the speed of light is .8 ca because, for a photon to move along the y axis of B, it must have a component of its 1 ca velocity through the qm be .6 ca in the +x direction in order to keep up with B's motion through the qm. This is shown by the vector diagram where ca is the velocity of the light through the qm, va is the velocity of B through the medium and cr is the velocity of the light relative to B. For any velocity va of frame B, the speed of light cr along the y axis is cr=(1−va).

     In frame A the speed of light along the y axis is 1 ca. Therefore, the light clocks on A keep absolute time and 1 s on A's clocks is 1 sa. But on B, where the speed of light in any direction perpendicular to va is cr=.8 ca, the clocks advance at only .8 times the rate of clocks aboard A.

     Prior to frame B arriving at frame A, the observers(c) at the origins of the frames set their clocks so that when the origin of B is momentarily next to the origin of A (at time ta=0 sa) both clocks will read 0 s. For example, when the origin of frame B is 600 ls from the origin of A and moving toward A with velocity v=.6 c, the observers(c) set their clocks to read −1000 s because they know that it will take 1000 s on their clocks before the origins meet.

     Then the observers at the other distance marks along the x and y axes of A and B synchronize their clocks with the clock at the origin of their spaceframe. They do this by setting their clocks D s later than the time they see on their origin clock, where D is their distance in ls from their origin clock. For example, observers at the .5 ls locations along the x and y axes set their clocks to read .5 s later than the time they see on their origin clock because they believe that the light from the origin clock takes .5 s to reach them. This virtual synchronization of the clocks results in the absolute synchronization of the clocks in frame A where the speed of light is the same in all directions, as the observers(c) believe. But in frame B the speed of light is not constant, and only the clocks along the y axis of B are absolutely synchronized with the origin clock. The simple rule (left) helps determine the asynchronization between two clocks in any inertial frame.