A body's variable mass/energy due to its changing internal energy
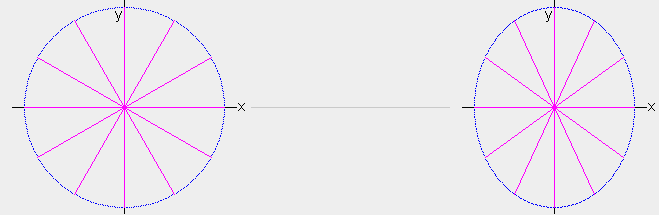
     To analyze how the internal energy in a body changes as the body's absolute velocity va is increased, we can imagine a body consisting of an energy source that radiates photons at the center of a massless spherical shell that has a 1 ls radius and is initially at rest in the qm (left figure). The inside surface of this huge shell absorbs and reemits photons back to the center where the energy is absorbed and reemitted. To further simplify our analysis, we will consider only the photons moving in the x-y plane of the sphere's x-y-z coordinate system. At every second on a clock at the origin, a photon is emitted along the x axis and 11 other photons are emitted at angles of 30°, 60°, 90°, 120°, ... 330° to the x axis. After two seconds there are 24 photons. Twelve have just been emitted at the center of the imaginary body and 12 have just been absorbed and reemitted at the spherical surface 1 ls away. The photons all have the same oscillation frequency and an energy that we will designate 1 ep. Therefore, the total at-rest mass/energy of the 24-photon system is 24 ep.

     The entire system is then accelerated to velocity va=.6 ca in the +x direction (right figure). The sphere's 1 ls radius along the x axis is now .8 LS and what appears to be 30, 60, and 90 degree angles to observers(c) in the sphere are absolute angles of 35.8, 65.2, and 90 degrees. Because rv=.8 for the system, the emission frequency is only .8 times the at-rest frequency and photons are now emitted every 1.25 sa, which is every 1 s on the system's clocks. In spite of the lower emission frequency and lower rate of emission, we will see that the photons have more energy due to the system's velocity through the qm. They have exactly the additional energy to account for the observed increase in a body's mass when accelerated to the high velocity.